Accuracy of latitude and longitude measurements?
Accuracy is the tendency of your measurements to match true values. Accuracy is the degree to which your measurements determine the actual value. It is about the interplay of accuracy and precision.
Generally, you don't need much more precision in recording your measurements than the precision built into them. Using too much precision can mislead people into thinking the precision is greater than it actually is.
Typically, when you reduce precision, that is, use fewer decimal places, you may lose some precision. How much? It's good to know that the meter was originally defined (by the French, around the time of their revolution, when they were throwing out the old systems and diligently replacing them with new ones) so that ten million of them will take you from the equator to the pole. It's 90 degrees, so one degree of latitude covers about 10^7/90 = 111,111 meters. ("Approximately" because the length of the meter has changed a little during this time. But that doesn't matter.) Also, the degree of longitude (east-west) is about the same or smaller in length than the degree of latitude because the circles of latitude are compressed to the axis earth when we move from the equator to either pole. Therefore, it is always safe to assume that the sixth decimal place in one decimal degree has 111.111/10^6 = about 1/9 meter = about 4 inches of precision.
Accordingly, if your precision requirement is, say, to give or take 10 meters, then 1/9 of a meter is nothing: you essentially lose no precision by using six decimal places. If your accuracy is less than a sub-centimeter, then you need at least seven and perhaps eight decimal places, but nothing else will do.
Thirteen decimal places would peg this location at 111.111/10^13 = about 1 angstrom, about half the thickness of a small atom.
Using these ideas, we can make a table of what each decimal digit means:
- The sign tells us whether we are north or south, east or west on the globe.
- A non-zero digit in the hundreds tells us that we are using longitude, not latitude!
- Tens of numbers give a position of about 1000 kilometers. This gives us useful information about what continent or ocean we are on.
- The units digit (one decimal power) gives a position of up to 111 kilometers (60 nautical miles, about 69 miles). This can tell us roughly what large state or country we are in.
- The first decimal place is up to 11.1 km: it can distinguish the position of one large city from a neighboring large city.
- The second decimal place is up to 1.1 km: it can separate one village from others.
- The third decimal place is up to 110 m: it can identify a large agricultural field or an institutional campus.
- The fourth decimal place is worth up to 11 m: it can define a piece of land. This is comparable to the typical accuracy of an uncorrected GPS unit without interference.
- The fifth decimal place is up to 1.1 m: this is to distinguish trees from each other. Accuracy to this level with commercial GPS devices can only be achieved using differential correction.
- The sixth decimal place is up to 0.11 m: you can use this for laying out structures in detail, for designing landscapes, building roads. This should be more than enough to track the movement of glaciers and rivers. This can be achieved by taking careful measures with GPS, such as GPS with differential correction.
- The seventh decimal place is up to 11 mm: this is good for large surveys and near borders, which GPS-based methods can achieve.
- The decimal place is up to 1.1 mm: this is good for plotting the movement of tectonic plates and the movements of volcanoes. Permanent, fixed, always-on GPS base stations may be able to achieve this level of accuracy.
- The ninth decimal place is up to 110 µm: we get in the microscopy range. For almost every possible application with ground positions this is overkill and will be more accurate than the accuracy of any surveying device.
- Ten or more decimal places indicate that a computer or calculator was used and that no attention was paid to the fact that additional decimal places are of no use. Be careful because if you do not read these numbers from the device, it may indicate poor processing quality !
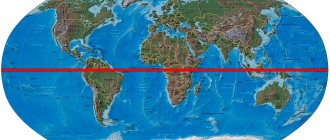
Equator length
You can also understand which parallel is the longest by looking at the specific values of the geometric dimensions of the geoid. The radius of the equator, as a circle “drawn” along the surface of the Earth, is equal to the radius of the planet. Precise measurements show that this parameter varies at different points on the planet - the polar radius is 21.3 km less than the equatorial one. Average value - 6371 km
Using the formula for circumference - 2πR - you can calculate the length of the equator. Different geophysical standards define figures with a difference of about 3 m, on average - 40075 km. along the meridian - 40,007 km, which proves the special geometric qualities of the geoid.
Best articles: American Foxhound is one of the oldest hound breeds
At what speed does the Earth rotate?
It's no secret that the change of day and night is technically caused by the rotation of the Earth around its axis. But has it ever occurred to you how fast it rotates? And how to calculate this speed? In general, if we talk about movement in a circle, there are two speeds: angular (ω) and linear (v). Let's try to find both.
Angular velocity of the Earth's rotation.
Angular velocity determines how quickly an angle changes over time. Since one full revolution corresponds to an angle of 360° or 2π, and the time during which it is completed is the period T, the angular velocity can be expressed as:
ω=2π/T
We know that there are 24 hours in a day, and, therefore, we can assume that the period of rotation of the Earth around its axis T will also be 24 hours. But don’t rush to convert this time into seconds and substitute it into the equation written above. Since the Earth still rotates around the sun, its period of revolution around its own axis will be slightly shorter than the solar day we are accustomed to and will be 23 hours 56 minutes and 4 seconds. This is the so-called sidereal day. In terms of seconds we get: T=86164 s.
Now you can find the angular velocity:
ω = 2π/T = 0.00007292115078 s-1
Linear speed
If we talk about angular velocity, then it is the same for any point on our planet
And it doesn’t matter: a penguin in the Arctic, an elephant in Africa or you at home, everyone will have the same angular velocity. But when it comes to linear speed, it’s the other way around.
It will be maximum at the equator and decrease towards the poles, since it directly depends on the radius of the circle of rotation. This means that if you climb onto a stool to screw in a light bulb, your linear speed will increase. Strictly speaking, linear speed rather than describes the rotation of the Earth around its axis, it describes the rotation of some of its individual points.
Best articles: The strangest and most incredible facts about animals
Calculating linear speed is very simple. By definition, speed is the ratio of the distance traveled to the time during which this path was completed. If in one revolution we cover a path equal to the length of the circle, and the time of movement is nothing more than the period of revolution T, then, by expressing the length of the circle from the well-known school formula: L = 2πR, we obtain an equation for calculating linear speed:
V= 2πR/T
Since the angular velocity ω = 2π/T, we can safely write:
V=ωR
The radius of the earth at the equator is R = 6378245 m, which means the linear speed there will be equal to:
V≈465 m/s
If we convert this value into kilometers per hour, we get 1674 km/h!!! Decent speed. But this is on the equator, somewhere in hot Africa, its central part. Closer to the poles the value will be lower. So, for example, for St. Petersburg the linear speed will be half the equatorial speed, only 837 km/h, and at the poles it will be 0 km/h.
What happens if…?
What happens if the earth stops rotating? Are you familiar with the situation when you are traveling on a crowded bus, suddenly the driver suddenly brakes at a traffic light, and all the passengers, including you, fly...??? Where? It’s clear where to go, hug the driver and kiss the windshield. About the same thing will happen if the Lord God hits the brakes and stops the Earth. But if the speed of the bus is 60 km/h, then in the case of the Earth the numbers are completely different. The value of 1674 km/h is comparable to the speeds of supersonic aircraft. Namely, it is at these speeds that all bodies and objects located on the surface of the earth will begin to move in the event of an emergency stop. Of course, in Russia, due to the fact that the country is located in northern latitudes, the speeds will be lower, but it will still be possible to accelerate the Zhiguli 6 model to 837 km/h!!! We just need to stop the Earth.
What will happen if the Earth starts to rotate faster? Everyone knows that the Earth is not exactly a sphere; it is slightly flattened at the poles, which is due to its rotation around its axis. Increasing the rotation speed will flatten our Earth even more. At a speed sufficient for this, it may well turn into a pancake and really become flat. Also, an increase in speed can lead to the fact that all bodies located on its surface will fly into space. For this, it is necessary that the linear speed of these bodies exceed the second cosmic speed (11.2 km/s). And who knows, maybe someday Mother Earth will get tired of our stupid attempts to control her and, finally, add momentum, scattering us throughout the solar system.